확률
경험 혹은 실험의 결과로 특정한 사건이나 결과가 발생할 가능성이다.
확률의 기초 개념
확률에 대한 기본적인 용어로는 두 가지만 알면 된다.
표본 공간(S, Sample space)
표본 공간은 '통계적 조사에서 얻을 수 있는 모든 가능한 결과들의 전체 집합'이다.
영어로는 'The set of possible outcomes'로 해석하면 '가능한 모든 수'이다.
한 상황에 대해 우리가 생각해 볼 수 있는 모든 결과를 표본 공간이라고 한다.
표본 공간은 집합이다. 흔히 앞글자를 따 S라고 표기한다. S = {A, B, C}라고 쓰면 표본 공간을 표기한 것이다. 그러면 표본 공간이라는 집합의 각 원소는 바로 각각의 경우가 되는 것이다.
여기서 중요한 것은 표본 공간의 원소들은 절대 숫자가 될 필요가 없다는 것이다. 숫자든, 상황이든 괜찮다. 집합이어도 된다.
사건(E, Ecent)
사건은 위의 표본 공간을 이해하면 쉽게 생각할 수 있다.
표본 공간의 부분 집합이 사건이다. 무슨 뜻인지 예를 들면, 주사위를 던지는 경우 나오는 숫자는 1, 2, 3, 4, 5, 6이 있을 것이다. 이때 전체 경우는 1, 2, 3, 4, 5, 6이니 표본 공간은 {1, 2, 3, 4, 5, 6}이 된다. 근데 나는 홀수가 나왔으면 좋겠다고 생각할 경우 홀수가 나오는 사건은 {1, 3, 5}가 된다. 6이 나오면 좋겠다고 생각하면 사건은 {6}이 된다.
사건 역시 수학적으로 집합이라 꼭 괄호 표시를 해야 한다.
확률의 정의
통계학은 크게 두 가지 학파로 나뉜다.
동전을 던졌을 때 앞면이 나올 확률은?이라고 질문하면 거진 대부분 1/2라고 대답할 것이다. 이것이 바로 Frequentist의 관점이다. 확률의 정의에 따라 앞면이 나올 확률은 1/2라고 논리적으로 귀결시키는 것이다. 하지만 Bayesian은 대답이 제각각이다. 그 이유는 Bayesian 확률의 경우 축적된 배경지식에 의해 확률이 변할 수 있다고 생각하기 때문이다.
그렇기 때문에 확률의 정의도 두 관점에 따라 두 가지로 나뉘지만 따로 언급하지 않는 한 잘 등장하지 않기 때문에 Frequentist의 관점만 견지해도 괜찮다.
Frequentist의 정의
수학자 라플라스는 확률을 이렇게 정의했다.
N개의 원소로 구성된 표본공간 S가 있다고 했을 때, 각각의 원소(근원사건)가 일어날 가능성이 모두 같다고 가정할 수 있을 때, n개의 원소로 구성된 사건 A가 일어날 확률은 P = n/N과 같다고 말이다.
그러나 P = n/N이라는 고전적 정의는 말이 안 된다.
예를 들어 경품 행사의 상품이 {아이폰, 문화상품권, 머그컵, 꽝}인 경우 1등 경품의 사건은 {아이폰}이다. 이때 고전적 정의는 1등부터 4등까지 뽑힐 확률이 1/4라고 주장하는 것이다.
예시처럼 단순한 기준을 가지고 확률을 계산하면 효과적이지 못할 것이다. 왜냐하면 근원사건이 일어날 가능성이 모두 같기는 힘들기 때문이다. 또, 중요한 것은 조사 대상이 무한한 경우는 생각하지 않고 있다는 것이다. 이렇게 '근원사건의 일어날 가능성이 모두 같기 힘들다'와 '조사 대상이 유한한 경우에만 한정하고 있다'라는 두 가지 측면에서 확률의 고전적 정의는 한계에 부딪힌다.
그러자 수학자 콜모고로프가 더 유용한 정의를 제안했다.
바로 콜모고로프의 확률의 공리적 정의이다. 바로 상대도수의 극한을 말하는 것이다.
콜모고로프는 다음 세 가지 규칙을 세운다.
- 0 ≤ P(A) ≤ 1
- P(S) = 1
- P(A∪B∪...) = P(A) + P(B) +...
이 세 가지 조건을 만족하는 사상 P를 확률이라고 정의한다. 이 사상(mapping)은 쉽게 함수라고 생각하면 된다.
1번과 2번은 상당히 직관적이다. 확률을 흔히 0 이상 1 이하로 표현하고, 또 표본공간 S가 가능한 모든 수였으니까 가능한 모든 수의 확률은 당연히 1인 것이다.
그런데 3번은 새로운 용어 '배반'이 등장한다. 이 '배반'은 교집합이 공집합이라는 뜻이다.
즉, A와 B가 배반사건(exclusive)이라는 뜻은 A가 일어났다면 절대 B가 일어날 리 없고, B가 일어났다면 절대 A가 일어날 리 없다는 뜻이다. 한마디로 동시에 A와 B를 관찰할 수 없다는 말이다.
3번을 식으로 표현하면 A ∩ B = ∮ 으로 동시에 일어날 리 없는 두 사건 중 적어도 하나(합집합의 개념이다)가 일어날 사건은 두 사건이 일어날 확률은 더한 게 된다는 뜻이다.
참고 1.
배반(exclusive)과 상호배반(mutually exclusive)은 다르다.
배반은 두 사건 간의 배반의 성질을 말하고 상호배반은 여러 개의 사건이 있을 때 어떤 두 개를 골라도 서로 배반의 성질을 가지고 있을 때를 말한다. 3번의 경우 모든 사건끼리 배반인 경우, 즉 상호배반인 경우를 말하는 것이다.
참고 2. 배반과 독립은 다르다. 배반은 동시에 일어날 리 없는 사건이다. 쉽게 설명하면 서로 원수지간인 친구고 독립은 서로 모르는 친구다. 서로 무엇을 하든 상관없는 것이다.
Bayesian의 정의
Frequentist은 빈도를 중시한다. 즉, 빈도가 키워드다.
반면 Bayesian은 plausibility에서 출발한다. 가능성보다는 포괄적인 개념으로 '그럴듯함'을 표현한다.
좀 더 이해하기 쉽게 고등학교 1학년 수학 집합과 명제 단원으로 돌아가 예제를 보면 아래와 같다.
- A → B(A이면 B이다)가 참일 때, A가 참이면 B가 참이다.
- A → B가 참일 때, B가 거짓이면 A가 거짓이다.
- A → B가 참일 때, B가 참이면 A는 더욱 그럴싸하다.
- A → B가 참일 때, A가 거짓이면 B는 덜 그럴싸하다.
- A가 참일 때 B가 더욱 그럴싸한 것이 참이라면, B가 참일 때 A는 더욱 그럴싸하다.
1번은 너무 당연하고 2번은 대우 명제가 참인 것이다.
3번에서 5번까지는 common sense(상식)에는 부합하지만 논리적으로는 옳지 않은 것이다. 예를 들어 어떤 친구가 직전 시험까지 전교 1등이라고 했을 때, 요번 시험의 전교 1등은 누굴까라고 물으면 모두 그 친구를 떠올릴 것이다. 물론 그 친구가 전교 1등이라는 논리적 근거는 없다. 하지만 그 친구가 전교 1등인 것이 제일 그럴싸한 것이다. 바로 이 것이 3번부터 5번까지의 statement이다.
common sense(상식)의 가정
- 하나의 경우에는 한 가지 값에 대응된다.
- common sense(상식)에 부합한다.
- consistency 즉, 이론 전개에 있어 일관성을 가진다.
Bayesian은 common sense의 가정을 포함시켜 확률을 정의한다.
common sense의 가정 1번과 2번을 가지고 우리가 흔히, 그리고 당연하게 알고 있는 곱셈 법칙과 덧셈 법칙을 유도하고 maximum entropy 등을 가정으로 3번을 만족시켜 결국 확률이라는 하나의 개념을 유도해 냈다.
확률의 종류
주관적 확률
의사결정저가 자신의 지식이나 경험에 의거하여 주관적으로 어떤 사건이 일어날 가능성에 부여한 일정한 값을 말한다.
주관적 확률은 개인의 경험에 바탕을 둔, 말 그대로 주관적이기 때문에 소위 말하는 뇌피셜이라는 생각이 들 수 있다. 그러나 이 개인의 판단에 새로운 정보가 지속적으로 들어옴으로써 판단이 올라가고, 정확도를 개선해 나가면 주관적 확률이 오히려 획기적인 지표가 될 수 있다.
객관적 확률
특정 사건이 발생할 가능성이 객관적으로 명확하여 누구나 쉽게 알 수 있는 경우나 동일한 실험을 무수히 반복적으로 수행할 경우 특정한 사건이 발생할 확률이다.
- 고전적 확률
- 이론에 근거한 사전 확률이다.
- 모든 결과가 발생할 가능성이 명확하고, 각 결과는 서로 배타적이다. 즉, 서로 다른 2개 이상의 결과가 동시에 발생할 수 없는 경우 활용한다.
- 장기적 상대도수 확률
- 실제 실험에 근거한 사후 확률이다.
- 같은 실험을 반복적으로 무수히 수행할 경우 특정 사건이 발생할 수 있는 상대적 빈도로 정의한다.
한계 확률(주변 확률)
2개의 변수가 교차되어 만들어진 빈도교차상에서 하나의 관측치가 행이나 열 어느 한 변수에 의해서만 구분되는 특정 집단에 속할 확률을 말한다. 즉, 개별 사건의 확률이지만 결합 사건들의 합으로 표시될 수 있는 확률을 의미한다.

위의 표를 이용해 상세히 설명하자면 한계 확률은 표에서 각 행의 확률의 합과 각 열의 확률의 합을 더하는 것이므로 상위 20위 대학의 MBA 학위를 취득한 사람이 뮤추얼 펀드의 수익률이 시장수익률보다 높을 확률과 상위 20위 대학의 MBA 학위 취득한 사람이 뮤추얼 펀드의 수익률이 시장수익률보다 높지 않을 확률을 구한다면 0.40이라는 확률을 기록할 것이다. 이런 방식으로 한계 확률을 구하면 아래와 같다.
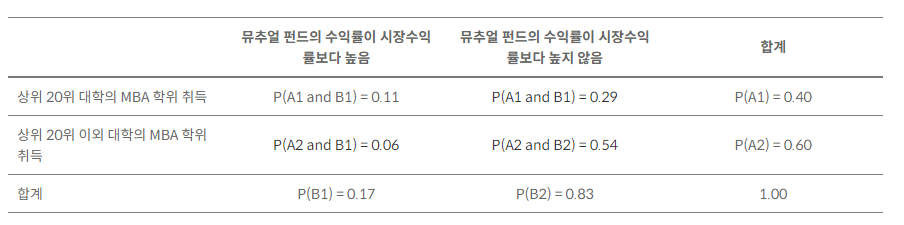
결합 확률
두 개 이상의 사건이 동시에 발생할 가능성을 나타내는 확률이다. 다르게 설명하면 서로 배반되는 두 사건 A, B가 있을 때 두 사건이 동시에 일어날 확률을 P(A∩B)라고 한다.
조건부 확률
이미 하나의 사건이 발생한 상태에서 또 다른 사건이 발생할 가능성을 나타내는 확률이다. 즉, 어떤 사건 A가 일어났다는 전제 하에서 사건 B가 발생할 확률을 말한다.
조건부 확률은 통상적으로 P(A|B)로 표현된다. 여기서 B가 조건이다.
공식으로 보면 P(A|B)=P(A교집합 B)/P(B)가 된다. 변형적으로 P(A교집합 B)=P(A|B) P(B)=P(B|A) P(A)가 성립하게 된다.
확률의 연산 법칙
덧셈법칙
사건이 있을 때 서로 배반인 경우 서로 배반인 모든 사건에 대한 교집합 즉, 모든 사건이 일어날 확률은 각 사건이 일어날 확률의 합과 같다.
조금 더 쉽게 말하자면 사건이 동시에 일어나지 않을 때는 '사건 A 또는 사건 B가 일어날 확률 = (사건 A가 일어날 확률) + (사건 B가 일어날 확률)'처럼 각각의 확률을 더해주면 되는 것이다.
곱셈법칙
사건이 있을 때 독립, 여러 사건이 있을 때 서로 독립할 때만 해당된다.
서로 독립인 모든 사건에 대해 교집합 즉, 모든 사건이 일어날 확률은 각 사건이 일어날 확률의 곱과 같다.
조금 더 쉽게 설명하자면 두 사건이 동시에 일어날 때 '사건 A와 사건 B가 동시에 일어날 확률 = (사건 A가 일어날 확률) x (사건 B가 일어날 확률)'처럼 각각의 확률을 곱해서 계산하는 것이다.
확률 변수
확률은 경험 혹은 실험의 결과로 특정한 사건이나 결과가 발생할 가능성이라면 변수는 관심 대상의 속성을 척도를 이용하여 측정한 값들을 대표하는 것이다. 즉, 확률 변수는 특정한 값을 가질 수 있는 확률이 주어진 변수를 말한다.
조금 더 쉽게 말하자면, 확률 변수는 그냥 변할 수 있는 수다. 여기서 그냥 변수와의 차이점은 확률을 가지고 값이 결정된다는 점이다. 변수는 그 수가 무엇이 될지 확률적으로 예측이 불가능하지만 확률 변수는 정해진 확률에 따라 확률 변수의 값이 결정된다.
또한, 확률 변수는 변'수'이므로 표본 공간의 각 원소를 실수 값으로 대응시킨다. 예를 들어 훈련병을 0, 상병을 1, 소위를 2라고 정하고 0, 1, 2를 표현하는 확률 변수 X를 서든어택 계급이라고 정의해서 표현하는 것이다. 그렇기 때문에 다분히 주관적이고 임의로 정할 수 있다.
확률 변수의 종류는 아래와 같다.
- 이산 확률 변수
- 정수와 같이 명확한 값을 변수 값으로 한다.
- 확률 변수가 가질 수 있는 값의 수가 한정되어 그 수를 셀 수 있는 변수다.
- 확률 변수가 어느 구간의 모든 실수값을 택하지 않고 고립된 값만 택한다.
- 상태 공간이 유한 집합인 또는 셈할 수 있는 무한 집합인 확률 변수를 말한다.
- 딱딱 끊어진 또는 구분된 변수로 구성되어 있다.
- 동전 던지기 게임이나 주사위 던지기 게임이 대표적인 이산 확률 변수다.
- 연속 확률 변수
- 변수 값이 정수처럼 명확하지 못하다.
- 확률 변수가 연속량으로 표기되어 가능한 변수 값의 개수를 셀 수 없는 변수다.
- 확률 변수가 취하는 값이 연속된 구간으로 나타나는 것을 말한다.
- 연속적으로 이어진 변수로 이루어져 있다.
- 정규 분포가 대표적인 연속 확률 변수다.
확률 이론 기초 코드 공부
< 추후 추가 예정 >
참고 자료
- http://kocw-n.xcache.kinxcdn.com/data/document/2020/pusancatholic/parkmanhee0727/3.pdf
- https://stementor.tistory.com/entry/%ED%86%B5%EA%B3%84%EB%9E%91-2%EC%9D%BC%EC%A7%B8-%EA%B8%B0%EC%B4%88%ED%99%95%EB%A5%A0%EB%A1%A0-1
- https://stementor.tistory.com/entry/%ED%86%B5%EA%B3%84%EB%9E%91-2%EC%9D%BC%EC%A7%B8-%EA%B8%B0%EC%B4%88%ED%99%95%EB%A5%A0%EB%A1%A0-1
- https://stementor.tistory.com/entry/%ED%86%B5%EA%B3%84%EB%9E%91-3%EC%9D%BC-%ED%99%95%EB%A5%A0-%EB%B2%95%EC%B9%99%EA%B3%BC-%EC%A1%B0%EA%B1%B4%EB%B6%80-%ED%99%95%EB%A5%A0
- https://stementor.tistory.com/entry/%ED%86%B5%EA%B3%84%EB%9E%91-4%EC%9D%BC%EC%A8%B0-%ED%99%95%EB%A5%A0%EB%B3%80%EC%88%98%EC%99%80-%EB%AA%A8%EC%88%98-%EA%B7%B8%EB%A6%AC%EA%B3%A0-%ED%86%B5%EA%B3%84%EB%9F%89
- https://datalabbit.tistory.com/16
- https://drhongdatanote.tistory.com/49
- https://mathbang.net/114#gsc.tab=0
- https://kurt7191.tistory.com/10
- https://datalabbit.tistory.com/17
'공부일기 > 통계' 카테고리의 다른 글
| 신뢰 구간(Confidence Interval) (0) | 2024.08.16 |
|---|---|
| p-값(p-value)과 통계적 유의성(Statistical Significance) (0) | 2024.08.16 |
| 가설 검정(Hypothesis Testing) (0) | 2024.08.12 |
| 기술 통계 vs 추론 통계(Descriptive statistics vs Inferential statistics) (0) | 2024.08.11 |
| 확률 분포(Probability Distribution) (0) | 2024.08.11 |